（問 1/1 追加の問題）
(追加の問題です)
図のような三角形があります。
(追加の問題です)
図のような三角形があります。
正解です。 正解は 56 です。
∠x+∠y を求めなさい。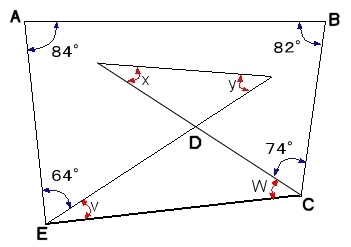
ＥからＣへ補助線を引くと
角Ｘ＋角Ｙ＝角Ｖ＋角Ｗ になる。
４角形の内角の和は１８０×２＝３６０度だから
Ｖ＋Ｗ＝３６０－（８４＋８２＋７４＋６４）
これは角Ｘ＋角Ｙに等しい
84+82+74+64=304°です。
それに∠x+∠y=360° になりますから、
360-304=56° となります。
もう一つの解法です。
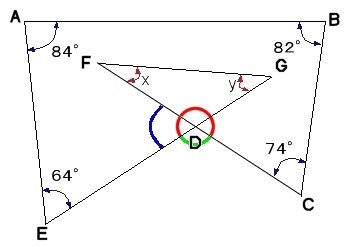
５角形の内角の和を求めてとく方法は順番に分かる角度を求めていくという基本的な方法だ
五角形の内角の和は、１８０×３＝５４０°
だから、赤い腺で表した角ＣＤＥは
５４０－（８４＋８２＋７４＋６４）＝２３６°
そこで、緑で表した角ＣＤＥは
３６０－２３６＝１２４度
青で表した角ＦＤＥは
１８０－１２４で計算できる。
これはｘ＋Ｙに等しい。
合格おめでとう。
次の問題へ進む
感想、エラー報告のお願い
ぜひ、ご協力お願い申し上げます。